
| Index A I | MNIST学習 |
|
MNIST学習 データセット SGD数値勾配 誤差逆伝播法 認識制度推移 SimpleConvNet 認識制度推移 深層学習 NW初期化 重み初期化 訓練開始 レイヤ生成 レイヤ遷移 入力の次元 NN機能・要件 NN構成・方式 構成・方式など タスク 導入 Sample 用語 |
MNIST学習 ・ニューラルネットワークの学習を行う。 重みパラメータの作成を行う。・学習の仕方 SGD 数値勾配 誤差逆伝播法 シンプルなCNN ディープラーニングMNIST のデータセット ・MNIST(エムニスト)のデータセット 指定保存場所に ダウンロード (mnist.py) |_mnist.py |_t10k-images-idx3-ubyte.gz |_t10k-labels-idx1-ubyte.gz |_train-images-idx3-ubyte.gz |_train-labels-idx1-ubyte.gz 解凍 し、データセット (mnist.py) それぞれのデータの形状 print (dataset['train_img'].shape) (60000, 784) print (dataset['train_label'].shape) (60000,) print (dataset['test_img'].shape) (10000, 784) print (dataset['test_label'].shape) (10000,) Pickle形式で 保存 (mnist.py) data ディレクトリに mnist.pkl 作成 画像表示 (mnistDataHyouji.py)   確率的勾配降下法 数値勾配によるミニバッチ学習実装 ・サンプル functions.py (関数) mnist.py (データセット) mnistNumerical_gradient.py (数値勾配ミニバッチ学習) TowLayerNet (2層ニューラルネットワーク)・2層ニューラルネットワークをクラスとして実装 入力層(0層)784個、 中間層(1層)50個、 出力層(2層)10個 勾配計算のメソッドは、 numerical_gradient・学習手順 重みパラメータに関する損失関数の勾配の、数値微分による算出 ニューラルネットワークの学習における勾配 重みパラメータを、損失関数の変数とする。(loss_W = lambda W:) 重みパラメータに関する損失関数(L)の勾配(∂L / ∂W) 数値微分によって
勾配を求める。 勾配を求める実装 (例 TowLayerNet) パラメータの更新 (数値微分によるによるミニバッチ学習) 勾配(∂L / ∂W)を小さくする。(性能の悪さを最小にする。) 勾配降下法を利用して学習する。・sampleの実行結果 実行過程は誤差逆伝播法と同じ 時間は、1エポックが誤差逆伝播法の1万数千倍程度(数時間)誤差逆伝播法によるミニバッチ学習実装 ・サンプル functions.py (関数) mnist.py (データセット) mnistGradient.py (誤差逆伝播法ミニバッチ学習) TowLayerNet (2層ニューラルネットワーク)・2層ニューラルネットワークをクラスとして実装 入力層(0層)784個、 中間層(1層)50個、 出力層(2層)10個 勾配計算のメソッドは、 gradient・学習手順 重みパラメータに関する損失関数の勾配の、誤差逆伝播法による算出 ニューラルネットワークの学習における勾配 パラメータの更新 (数値微分によるによるミニバッチ学習) 勾配(∂L / ∂W)を小さくする。(性能の悪さを最小にする。) 勾配降下法を利用して学習する。・sampleの実行結果 実行過程は数値微分と同じ (時間は、1エポック 約1 秒) >$ python mnistGradient.py
データ確認
x_train.shape (60000, 784)
t_train.shape (60000, 10)
x_test.shape (10000, 784)
t_test.shape (10000, 10)
one_hot_label=True
2層nnクラスの入力層は784、中間層は50、出力層は10
重みの初期化 weight_init_std 0.01
self.params['W1'].shape (784, 50)
self.params['b1'].shape (50,)
self.params['W2'].shape (50, 10)
self.params['b2'].shape (10,)
(self.params['W1'])[0, 0] 0.013982489063855533
(self.params['W1'])[783, 49] 0.0014241270276013208
(self.params['b1'])[0] 0.0
(self.params['W2'])[0, 0] 0.010867215970553377
(self.params['W2'])[49, 9] -0.0025184368799455116
(self.params['b2'])[0] 0.0
ハイパーパラメータ
勾配法によるパラメータの更新回数 10000
訓練データ数 60000
ミニバッチの数 100
学習率 0.1
1エポックの繰り返し数 600.0
iter_per_epoch 0
train acc, test acc | 0.09736666666666667, 0.0982
iter_per_epoch 600
train acc, test acc | 0.7778, 0.7853
iter_per_epoch 1200
train acc, test acc | 0.8721166666666667, 0.876
iter_per_epoch 1800
train acc, test acc | 0.8969333333333334, 0.8999
iter_per_epoch 2400
train acc, test acc | 0.9072166666666667, 0.9096
iter_per_epoch 3000
train acc, test acc | 0.9135333333333333, 0.9151
iter_per_epoch 3600
train acc, test acc | 0.9186666666666666, 0.9211
iter_per_epoch 4200
train acc, test acc | 0.9216333333333333, 0.9246
iter_per_epoch 4800
train acc, test acc | 0.9255833333333333, 0.9284
iter_per_epoch 5400
train acc, test acc | 0.9284833333333333, 0.9299
iter_per_epoch 6000
train acc, test acc | 0.93275, 0.9344
iter_per_epoch 6600
train acc, test acc | 0.9350166666666667, 0.9353
iter_per_epoch 7200
train acc, test acc | 0.93765, 0.9383
iter_per_epoch 7800
train acc, test acc | 0.93995, 0.9393
iter_per_epoch 8400
train acc, test acc | 0.9422666666666667, 0.9417
iter_per_epoch 9000
train acc, test acc | 0.9443666666666667, 0.9424
iter_per_epoch 9600
train acc, test acc | 0.94675, 0.9433
ミニバッチ学習_end
・sampleの認識制度推移 訓練データとテストデータに対する認識制度の推移 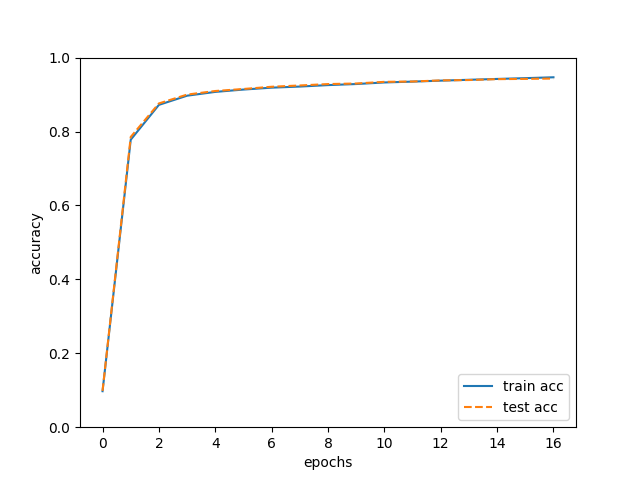 SimpleConvNetによる学習 ・サンプル functions.py (関数) layers.py (レイヤ) mnist.py (データセット) mnistSimpleConvNet.py (SimpleConvNetによる学習) optimizer.py (optimizer) simpleConvNet.py (SimpleConvNet) Trainer.py (ニューラルネットの訓練を行うクラス) util.py (util)・シンプルなConvNet実装 (SimpleConvNet) conv -
relu -
pool -
affine - relu - affine - softmax hidden_size=100, output_size=10, weight_init_std=0.01 conv_param = {'filter_num': 30, 'filter_size': 5, 'pad': 0, 'stride': 1}・sampleの実行結果 実行過程の時間は、1エポック 約90秒) $ python3 train_convnet.py
データ確認
x_train.shape (60000, 1, 28, 28)
t_train.shape (60000,)
x_test.shape (10000, 1, 28, 28)
t_test.shape (10000,)
重みの初期化
W1 (30, 1, 5, 5)
b1 (30,)
W2 (4320, 100)
b2 (100,)
W3 (100, 10)
b3 (10,)
レイヤの生成
self.layers[Conv1] <layers.Convolution object at 0x7f4a8f798080>
self.layers[Relu1] <layers.Relu object at 0x7f4a8cabc1d0>
self.layers[Pool1] <layers.Pooling object at 0x7f4a8cabc278>
self.layers[Affine1] <layers.Affine object at 0x7f4a8cabca20>
self.layers[Relu2] <layers.Relu object at 0x7f4a8cabc828>
self.layers[Affine2] <layers.Affine object at 0x7f4a8cabc9b0>
self.last_layer <layers.SoftmaxWithLoss object at 0x7f4a8cabc2e8>
optimizerは(Adam)
学習係数(lr)は 0.001
訓練クラス (Trainer)
エポック (self.epochs)は 20
ミニバッチサイズは(self.batch_size) 100
evaluate_sample_num_per_epoch(1000)
train_size(x_train.shape[0])は 60000
iter_per_epoch(60000/100)は 600.0
max_iter(20*600)は 12000
訓練開始
Convolution forward x.shape (100, 1, 28, 28)
Relu forward x.shape (100, 30, 24, 24)
Pooling forward x.shape (100, 30, 24, 24)
Affine forward x.shape (100, 30, 12, 12)
Relu forward x.shape (100, 100)
Affine forward x.shape (100, 100)
SoftmaxWithLoss forward x.shape (100, 10)
SoftmaxWithLoss backward
Affine backward
Relu backward
Affine backward
Pooling backward
Relu backward
Convolution backward
Convolution forward x.shape (100, 1, 28, 28)
Relu forward x.shape (100, 30, 24, 24)
Pooling forward x.shape (100, 30, 24, 24)
Affine forward x.shape (100, 30, 12, 12)
Relu forward x.shape (100, 100)
Affine forward x.shape (100, 100)
SoftmaxWithLoss forward x.shape (100, 10)
train loss:2.2995429548844437
Convolution forward x.shape (100, 1, 28, 28)
Relu forward x.shape (100, 30, 24, 24)
Pooling forward x.shape (100, 30, 24, 24)
Affine forward x.shape (100, 30, 12, 12)
Relu forward x.shape (100, 100)
Affine forward x.shape (100, 100)
同(forward)19回(「SoftmaxWithLoss」無し)
=== epoch:1, train acc:0.262, test acc:0.25 ===
以下、(forward)、(backward)、(forward)、(train loss:)の繰り返し
同(forward)20回(「SoftmaxWithLoss」無し)
=== epoch:2, train acc:0.xxx, test acc:0.xxx ===
以下、「epoch:20」まで繰り返し
以下、(forward)、(backward)、(forward)、(train loss:)の繰り返し
同(forward)100回(「SoftmaxWithLoss」無し)
train loss:0.0001884646933347338
Final Test Accuracy
test acc:0.9885
Saved Network Parameters!
SimpleConvNet学習_end
認識制度推移(SimpleConvNet) ・訓練データとテストデータに対する認識制度の推移 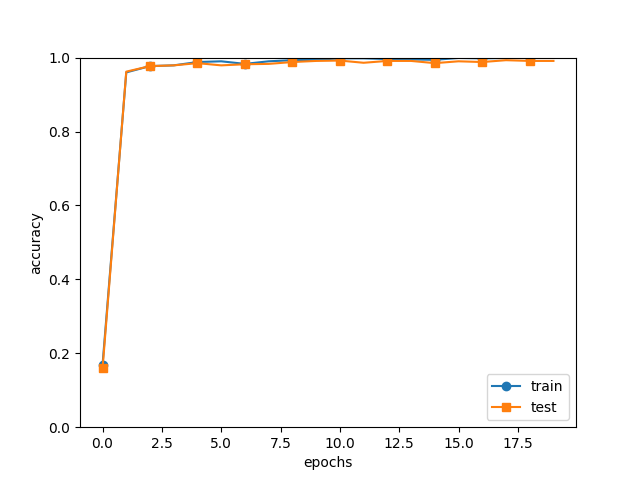 DeepConvNetによる学習 (MNIST用の多層ニューラルネットワークをクラスとして実装) ・サンプル deepConvNet.py (DeepConvNet) functions.py (関数) layers.py (レイヤ) mnist.py (データセット) mnistDeepConvNet.py (MNIST深層学習) optimizer.py (optimizer) Trainer.py (Trainer) util.py (util)・複雑なConvNet ・Convolutionレイヤ ・ニューラルネットの訓練を行うクラス ・sampleの実行経過(インテルi7の物理マシンで、2~3時間程度) $ python3 train_deepnet.py
データ読み込み (flatten=False)
ネットワーク構成 (DeepConvNet)
conv - relu - conv- relu - pool - conv - relu - conv- relu - pool -
conv - relu - conv- relu - pool - affine - relu - dropout -
affine - dropout - softmax
DeepConvNet__init__(ネットワーク初期化)
input_dim=(1, 28, 28)
convolutionエリアのフィルターの重み'filter_num','filter_size', 'pad', 'stride'
conv_param_1= {'filter_num': 16, 'filter_size': 3, 'pad': 1, 'stride': 1}
conv_param_2= {'filter_num': 16, 'filter_size': 3, 'pad': 1, 'stride': 1}
conv_param_3= {'filter_num': 32, 'filter_size': 3, 'pad': 1, 'stride': 1}
conv_param_4= {'filter_num': 32, 'filter_size': 3, 'pad': 2, 'stride': 1}
conv_param_5= {'filter_num': 64, 'filter_size': 3, 'pad': 1, 'stride': 1}
conv_param_6= {'filter_num': 64, 'filter_size': 3, 'pad': 1, 'stride': 1}
hidden_size=50
output_size=10
(ネットワーク初期化内、重みの初期化)
W = 初期値 * ガウス分布(フィルター数, チャネル数, フィルターサイズ, フィルターサイズ)
各層のニューロンひとつが、前層のニューロンといくつのつながりがあるか
pre_node_nums [ 9 144 144 288 288 576 1024 50]
ReLUを使う場合に推奨される初期値(weight_init_scales)
[0.47140452 0.11785113 0.11785113 0.08333333 0.08333333 0.05892557 0.04419417 0.2]
W は重みパラメータになれる。(前層のチャネル数とチャネル数は同じで、積算できる。)
Convolution結合(Affine結合ではない。)
self.params {}
入力のチャネル数 = input_dim[0]、 1
self.params['W1'].shape (16, 1, 3, 3)
self.params['W1'] [[[[-2.02614503e-01 1.54646178e-02 1.79391431e-01]
[-2.93400701e-01 -1.77965356e-01 -3.15000378e-01]
[ 6.13876118e-01 1.18367793e-01 -4.59401128e-02]]]
1~14チャネル、同様
[[[-8.58923210e-01 7.82185444e-01 -9.64429099e-02]
[ 1.26995494e+00 4.56541552e-01 -1.87158975e-01]
[-1.61923794e-01 1.30478209e+00 -5.80574250e-01]]]]
self.params['b1'] [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
W1のフィルター数(16)をpre_channel_numに設定
W2 (16, 16, 3, 3)
self.params['W2'] [[[[ 1.91905279e-01 2.02757865e-01 -2.87342926e-02]
[ 1.74964924e-01 -1.20009101e-01 1.49530269e-01]
[ 9.79308378e-03 3.43446511e-02 3.51302212e-02]]
・・・・
[[-0.04732913 0.01294622 0.0335121 ]
[-0.17892046 0.01101699 0.03202588]
[-0.03837846 -0.09724487 -0.0838004 ]]]]
b2 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
W2のフィルター数(16)をpre_channel_numに設定
W3 (32, 16, 3, 3)
self.params['W3'] [[[[ 0.06557074 -0.02819238 -0.01845345]
[-0.0151199 -0.02190891 0.01433862]
[ 0.03769021 -0.02830693 -0.00827718]]
・・・・
[[ 0.07987249 0.10145531 -0.01749849]
[-0.14744825 -0.02180667 -0.10978253]
[-0.11749816 -0.16667382 0.04836237]]]]
b3 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0.]
W3のフィルター数(32)をpre_channel_numに設定
W4 (32, 32, 3, 3)
self.params['W4'] [[[[ 2.13127146e-02 7.14255839e-03 2.26511155e-02]
[-4.29966555e-02 7.28521039e-02 -6.41670924e-02]
[ 1.85909313e-02 2.91449556e-02 -2.66956427e-02]]
・・・・
[[-5.75077561e-02 2.28618426e-02 -7.55179804e-03]
[ 1.14258462e-02 -1.88841176e-02 -1.30251209e-01]
[ 1.56797473e-01 -9.08880373e-02 4.42026465e-02]]]]
b4 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0.]
W4のフィルター数(32)をpre_channel_numに設定
W5 (64, 32, 3, 3)
self.params['W5'] [[[[ 5.26452866e-02 -2.17153285e-02 -1.30333982e-01]
[-8.19090563e-02 -6.17362840e-02 5.08962160e-02]
[ 1.44661174e-01 1.14347993e-01 1.77478525e-02]]
・・・・
[[ 1.76692912e-01 5.98875964e-02 8.63778253e-02]
[ 1.07203423e-01 -1.11469524e-01 3.63111351e-02]
[-4.30825622e-02 -1.30772913e-01 1.17487350e-02]]]]
b5 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
W5のフィルター数(64)をpre_channel_numに設定
W6 (64, 64, 3, 3)
self.params['W6'] [[[[ 0.0912546 -0.04262691 0.02487736]
[ 0.0821647 -0.02609576 0.11188648]
[-0.09871852 -0.03629912 -0.03841551]]
・・・・
[[ 0.03373332 0.04306996 -0.06825551]
[-0.06076129 -0.01639624 0.03234572]
[ 0.03313203 -0.05359558 0.03408823]]]]
b6 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
W7= weight_init_scales[6](0.04419417) * np.random.randn(64*4*4, hidden_size)
W7 (1024, 50)
W7 [[-0.01083619 0.01355946 -0.03149526 ・・・ -0.04653788 -0.00672065
-0.01497418]
・・・・
[ 0.0408319 -0.01565431 -0.06455872 ... -0.06308621 -0.08767341
0.04769704]]
b7 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.
0. 0.]
W8= weight_init_scales[7](0.2) * np.random.randn(hidden_size, output_size)
W8 (50, 10)
W8 [[ 1.88327124e-01 -8.73956843e-02 -7.43030570e-03 3.34721844e-02
-2.32227456e-01 1.64520538e-01 1.87530290e-01 9.87450536e-03
1.75083043e-02 -8.89778290e-02]
・・・・
[-4.85487788e-02 -3.25322340e-01 -3.23975960e-01 -5.49866777e-01
2.06118235e-01 7.13430832e-02 1.97618377e-01 3.50369312e-01
-6.36053526e-02 3.10088520e-01]]
b8 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
(ネットワーク初期化内、レイヤの生成)
self.layers = []
self.layers.append(Convolution(self.params['W1'], self.params['b1'],
conv_param_1['stride'], conv_param_1['pad']))
self.layers.append(Relu())
self.layers.append(Convolution(self.params['W2'], self.params['b2'],
conv_param_2['stride'], conv_param_2['pad']))
self.layers.append(Relu())
self.layers.append(Pooling(pool_h=2, pool_w=2, stride=2))
self.layers.append(Convolution(self.params['W3'], self.params['b3'],
conv_param_3['stride'], conv_param_3['pad']))
self.layers.append(Relu())
self.layers.append(Convolution(self.params['W4'], self.params['b4'],
conv_param_4['stride'], conv_param_4['pad']))
self.layers.append(Relu())
self.layers.append(Pooling(pool_h=2, pool_w=2, stride=2))
self.layers.append(Convolution(self.params['W5'], self.params['b5'],
conv_param_5['stride'], conv_param_5['pad']))
self.layers.append(Relu())
self.layers.append(Convolution(self.params['W6'], self.params['b6'],
conv_param_6['stride'], conv_param_6['pad']))
self.layers.append(Relu())
self.layers.append(Pooling(pool_h=2, pool_w=2, stride=2))
self.layers.append(Affine(self.params['W7'], self.params['b7']))
self.layers.append(Relu())
self.layers.append(Dropout(0.5))
self.layers.append(Affine(self.params['W8'], self.params['b8']))
self.layers.append(Dropout(0.5))
self.last_layer = SoftmaxWithLoss()
ネットワーク (DeepConvNet)
optimizerは(Adam)
学習係数(lr)は 0.001
訓練クラス (Trainer)
エポック (epochs)は 20
ミニバッチサイズは(batch_size) 100
evaluate_sample_num_per_epoch (1000)
train_size(x_train.shape[0])は 60000
iter_per_epoch(60000/100)は 600.0
max_iter(20*600)は 12000
訓練開始 max_iter回、train_step(self)実施
(6万の訓練データからランダムに1束(100個)取得、600回で1エポック、20エポック実施)
1束(100個、x_batch.shape=(100.1.28.28)、t_batch.shape=(100.))取得
1束(100個)に、gradient() 実施
gradient()
loss()
predict()
各レイヤのforward結果を取得
最初のConvolution forward
インプット x.shape (100, 1, 28, 28)→N, C, H, W
重み W1.shape (16, 1, 3, 3)→ FN, C, FH, FW
レイヤの遷移とニューロンへの入力
Convolution forward x.shape (100, 1, 28, 28)
Relu forward x.shape (100, 16, 28, 28)
Convolution forward x.shape (100, 16, 28, 28)
Relu forward x.shape (100, 16, 28, 28)
Pooling forward x.shape (100, 16, 28, 28)
Convolution forward x.shape (100, 16, 14, 14)
Relu forward x.shape (100, 32, 14, 14)
Convolution forward x.shape (100, 32, 14, 14)
Relu forward x.shape (100, 32, 16, 16)
Pooling forward x.shape (100, 32, 16, 16)
Convolution forward x.shape (100, 32, 8, 8)
Relu forward x.shape (100, 64, 8, 8)
Convolution forward x.shape (100, 64, 8, 8)
Relu forward x.shape (100, 64, 8, 8)
Pooling forward x.shape (100, 64, 8, 8)
Affine forward x.shape (100, 64, 4, 4)
Relu forward x.shape (100, 50)
Dropout forward x.shape (100, 50)
Affine forward x.shape (100, 50)
Dropout forward x.shape (100, 10)
SoftmaxWithLoss forward x.shape (100, 10)
レイヤのbackwardを逆に辿る。
SoftmaxWithLoss backward
Dropout backward
Affine backward
Dropout backward
Relu backward
Affine backward
Pooling backward
Relu backward
Convolution backward
Relu backward
Convolution backward
Pooling backward
Relu backward
Convolution backward
Relu backward
Convolution backward
Pooling backward
Relu backward
Convolution backward
Relu backward
Convolution backward
forward2回目
train loss:2.259148889493097
forward3回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward4回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward5回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward6回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward7回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward8回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward9回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward10回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward11回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward12回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward13回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward14回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward15回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward16回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward17回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward18回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward19回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward20回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward21回目、SoftmaxWithLossなし、レイヤのbackwardなし
forward22回目、SoftmaxWithLossなし、レイヤのbackwardなし
=== epoch:1, train acc:0.109, test acc:0.118 ===
forward1回目、SoftmaxWithLossあり
レイヤのbackwardを逆に辿る。
forward2回目、SoftmaxWithLossあり
train loss:2.346498438332875
forward1回目、SoftmaxWithLossあり
レイヤのbackwardを逆に辿る。
forward2回目、SoftmaxWithLossあり
train loss:2.294114848166848
forward1回目、SoftmaxWithLossあり
レイヤのbackwardを逆に辿る。
forward2回目、SoftmaxWithLossあり
train loss:2.3271042408576728
forward1回目、SoftmaxWithLossあり
レイヤのbackwardを逆に辿る。
forward2回目、SoftmaxWithLossあり
train loss:2.276695334729226
forward1回目、SoftmaxWithLossあり
レイヤのbackwardを逆に辿る。
forward2回目、SoftmaxWithLossあり
train loss:2.2695305787097393
・・・・
=== epoch:20, train acc:0.995, test acc:0.989 ===
train loss:0.8803254502136413
train loss:0.8300136406770576
train loss:0.9018399353626201
train loss:0.862232334277936
train loss:0.8245117918709284
train loss:0.7311440190827428
Final Test Accuracy
test acc:0.9944
Saved Network Parameters!
学習_end(正解率 99.4%)
|
| All Rights Reserved. Copyright (C) ITCL | |